The Time Formula

"Herb Furbus has been kidnapped by aliens!" These were the words that interrupted Dr. Pea's meticulous study of a dung beetle. He wasn't disappointed at having to stop his work, however--he had previously been trying to research time travel, but had gotten nowhere. A dung beetle study was second best at the moment. He turned around, pleased by the intrusion, and saw Norman Bufort running towards him holding a crumpled piece of paper.
"Hello, Norman! What can I do for you?"
"You can help me figure out what to do, Dr. Pea! I was on my way to Herb's house, and as I got there, an alien space ship came and took him away! All that was left was this piece of paper Herb had written on!" Norman handed Dr. Pea the piece of paper with the words "when I came" on them. Dr. Pea examined the paper, then turned it over.
"Great Scott!"
"What is it, Doc?"
"How could I have been so blind!? Look, here, on the back of the paper! Do you know what this is!?"
Norman Bufort looked on the back. It was a rather random looking math problem: 856 + 92 = Bundles.
"I have no idea," replied Norman.
"It's a formula!"
"How so?" Norman said. He wasn't exactly sure it was the best time for dissecting nonsensical math problems, but seeing as how he had no better course of action to get Herb back, he decided to humor the good doctor.
"It's the formula, Norman! The one I've been looking for! This is the formula that explains how to circumvent the space-time continuum in a 4-dimensionally efficient mechanism!"
"What?" said Norman, a rather confused expression stuck on his face.
"Let me break it down." Dr. Pea began to write quickly on his chalk board. "Look at it this way. Each letter in the alphabet corresponds to a number, where A=1, B = 2, Z = 26, right? Right. So, if this is the case, then you can reasonably assume that these numbers stand for letters. If you take 26 into 856, it goes into it 32 times with a remainder of 24. The 24th letter in the alphabet is X. If you do the same with 92, you get a remainder of 14, which is the letter N. Add up all the letters in B-U-N-D-L-E-S...2 + 21 + 14 + 4 + 12 + 5 + 19 = 77. Divide 26 into 77...remainder of 25...Y!! X + n = Y! That's the formula, where X = miles per second, n = the number of seconds, and Y = years! In theory, if we travel at 856 miles per second (which is approximately 2.5X the speed of sound), propelled against a sustained resistance for 92 seconds, we'll be able to create a time-vortex enabling us to travel four-dimensionally to an exact time and place! We're to travel 77 years into the past!"
"But 856 + 92 isn't 77! It's...uh...(carry the one)--"
"948. You're right. There's some correlation there. See, 948 divided by something must equal 77...which means...yes, yes...ah-ha! A = 948 / 77! A is our trajectory, or the angle at which the time machine must face when we "launch" so to speak!"
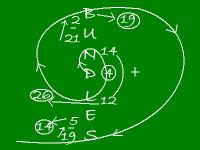"But we still don't know where to go!"
"I think we do! I think it's in this formula! See, if you draw Bentalagorus's Time Spiral over the word Bundles, this is what you come up with. D, of course, is equivalent to 4. If you add the L and the N, it equals 26 (14 + 12). Then, subracting top numbers from bottom numbers, you get U - B (21 - 2) and S - E ( 19 - 5)! We're to go to the city of Bundles on April 26, 1914! You said Herb wrote 'when I came' on the front of this paper, right? Right, so obviously, he wants us to travel to this place and this day in time! And this formula is how we'll do it!"
At that moment, Marcus came in through the door. "Where've you guys been!? I've been waiting for hours to go to Miller's!"
"Something's come up," replied Norman, "Herb's been abducted by aliens, and we have to go back in time to April 26, 1914 to save him or something..."
"Oh," Marcus said, "Okay. Well, I guess Miller's can wait."
"We'll need fuel once the time machine is complete," said Dr. Pea, "but I don't know where to get it."
"How do you know what fuel it needs?" asked Marcus.
"Easy," replied Dr. Pea, "X + n. Xn is another name for the element Xe, or Xenon. But I don't have any."
"I know where we can get some," replied Norman.